Forward & Backward Propagation
09 Dec 2022
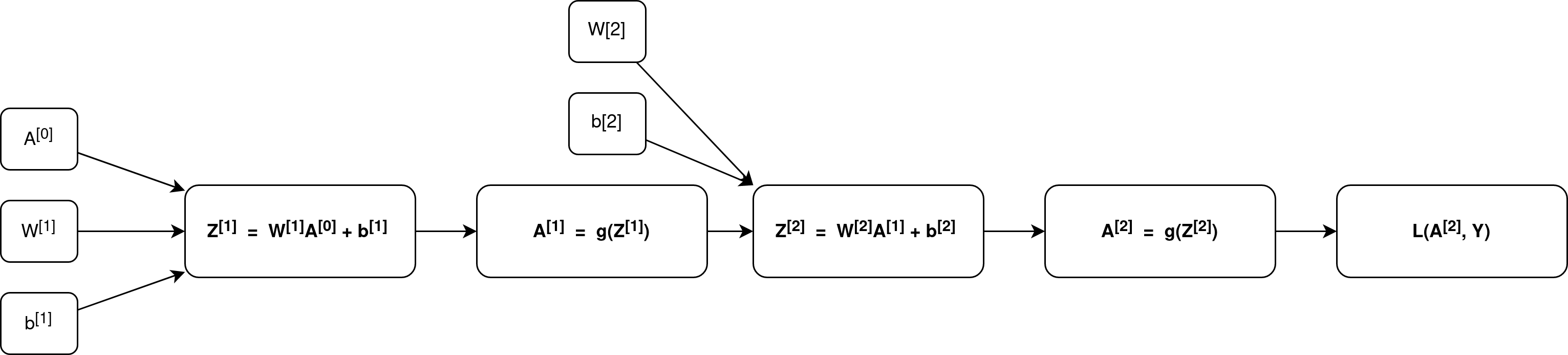
Forward Propagation
\[Z = WX + b\] \[Z = \begin{bmatrix*} z_{1}\\ z_{2} \end{bmatrix*} = \begin{bmatrix*} w_{11} & w_{12} & w_{13}\\ w_{21} & w_{22} & w_{23} \end{bmatrix*} \begin{bmatrix*} x_1\\ x_2\\ x_3 \end{bmatrix*} + \begin{bmatrix*} b_0\\ b_0 \end{bmatrix*}\] \[A = g(Z)\]For sigmoid,
\[A = \frac{1}{(1+ e^{-z^{[2]}})}\]Vectorized Form with m training set
\[Z = WX + b\] \[Z = \begin{bmatrix*} z_{11} && ... && z_{1m}\\ z_{21} && ... && z_{2m}\\ \end{bmatrix*} = \begin{bmatrix*} w_{11} & w_{12} & w_{13}\\ w_{21} & w_{22} & w_{23} \end{bmatrix*} \begin{bmatrix*} x_{11} & x_{12} & ... & x_{1m}\\ x_{21} & x_{22} & ... & x_{2m}\\ x_{31} & x_{32} & ... & x_{3m} \end{bmatrix*} + \begin{bmatrix*} b_0\\ b_0 \end{bmatrix*}\] \[A = g(Z)\]Backward Propagation
Loss function is given by
\[\begin{equation} L(A,Y)=-(Ylog(A) + (1-Y)log(1-A)) \end{equation}\]where final cost,
\[J(W,b) = (1/m)\sum_{i=1}^{m}{L(A, Y)}\]For backward propagation, we need to calculate \(\frac{\partial L}{\partial W^{[2]}}\), \(\frac{\partial L}{\partial b^{[2]}}\), \(\frac{\partial L}{\partial W^{[1]}}\) and \(\frac{\partial L}{\partial b^{[1]}}\) where we update
\[\begin{equation} W^{[2]} = W^{[2]} - \alpha \frac{\partial L}{\partial W^{[2]}} \end{equation}\] \[\begin{equation} b^{[2]} = b^{[2]} - \alpha \frac{\partial L}{\partial b^{[2]}} \end{equation}\] \[\begin{equation} W^{[1]} = W^{[1]} - \alpha \frac{\partial L}{\partial W^{[1]}} \end{equation}\] \[\begin{equation} b^{[1]} = b^{[1]} - \alpha \frac{\partial L}{\partial b^{[1]}} \end{equation}\]on each iteration
From chain rule,
\[\frac{\partial L}{\partial Z^{[2]}} = \frac{\partial L}{\partial A^{[2]}} \frac{\partial A^{[2]}}{\partial Z^{[2]}}\] \[\frac{\partial L}{\partial W^{[2]}} = \frac{\partial L}{\partial A^{[2]}} \frac{\partial A^{[2]}}{\partial Z^{[2]}} \frac{\partial Z^{[2]}}{\partial W^{[2]}} = \frac{\partial L}{\partial Z^{[2]}} (\frac{\partial Z^{[2]}}{\partial W^{[2]}})\] \[\frac{\partial L}{\partial b^{[2]}} = \frac{\partial L}{\partial A^{[2]}} \frac{\partial A^{[2]}}{\partial Z^{[2]}} \frac{\partial Z^{[2]}}{\partial b^{[2]}} = \frac{\partial L}{\partial Z^{[2]}} (\frac{\partial Z^{[2]}}{\partial b^{[2]}})\] \[\frac{\partial L}{\partial Z^{[1]}} = \frac{\partial L}{\partial A^{[2]}} \frac{\partial A^{[2]}}{\partial Z^{[2]}} \frac{\partial Z^{[2]}}{\partial A^{[1]}} \frac{\partial A^{[1]}}{\partial Z^{[1]}} = \frac{\partial L}{\partial A^{[1]}} (\frac{\partial A^{[1]}}{\partial Z^{[1]}})\] \[\frac{\partial L}{\partial W^{[1]}} = \frac{\partial L}{\partial A^{[2]}} \frac{\partial A^{[2]}}{\partial Z^{[2]}} \frac{\partial Z^{[2]}}{\partial A^{[1]}} \frac{\partial A^{[1]}}{\partial Z^{[1]}} \frac{\partial Z^{[1]}}{\partial W^{[1]}} = \frac{\partial L}{\partial Z^{[1]}} (\frac{\partial Z^{[1]}}{\partial W^{[1]}})\] \[\frac{\partial L}{\partial b^{[1]}} = \frac{\partial L}{\partial A^{[2]}} \frac{\partial A^{[2]}}{\partial Z^{[2]}} \frac{\partial Z^{[2]}}{\partial A^{[1]}} \frac{\partial A^{[1]}}{\partial Z^{[1]}} \frac{\partial Z^{[1]}}{\partial b^{[1]}} = \frac{\partial L}{\partial Z^{[1]}} (\frac{\partial Z^{[1]}}{\partial b^{[1]}})\]Let’s take each one and find it’s values.
\[\begin{equation*} \frac{\partial L}{\partial Z^{[2]}} = \frac{\partial L}{\partial A^{[2]}} \frac{\partial A^{[2]}}{\partial Z^{[2]}} \end{equation*}\] \[\frac{\partial L}{\partial A^{[2]}} = \frac{\partial}{\partial A^{[2]}}-(Ylog(A^{[2]}) + (1-Y)log(1-A^{[2]}))\] \[= -1*(Y*\frac{1}{A^{[2]}} + (1-Y)*\frac{1}{1-A^{[2]}}*-1)\] \[= \frac{-Y}{A^{[2]}} + \frac{1-Y}{1-A^{[2]}}\] \[= \frac{-Y+YA^{[2]}+A^{[2]}-A^{[2]}Y}{A^{[2]}(1-A^{[2]})}\] \[\boxed{ \begin{equation*} \frac{\partial L}{\partial A^{[2]}} = \frac{A^{[2]} - Y}{A^{[2]}(1-A^{[2]})} \end{equation*} }\] \[\frac{\partial A^{[2]}}{\partial Z^{[2]}} = \frac{\partial }{\partial Z^{[2]}}(\frac{1}{1+ e^{-z^{[2]}} }) = \frac{\partial }{\partial Z^{[2]}}(1+ e^{-z^{[2]}})^{-1} \\ = -1*(1+ e^{-z^{[2]}})^{-2}*e^{-z^{[2]}}*-1 \\ = \frac{e^{-z^{[2]}}}{(1+ e^{-z^{[2]}})^2} \\ = \frac{1}{(1+ e^{-z^{[2]}})} * \frac{e^{-z^{[2]}}}{(1+ e^{-z^{[2]}})} \\ = \frac{1}{(1+ e^{-z^{[2]}})} * \frac{1+e^{-z^{[2]}}-1}{(1+ e^{-z^{[2]}})} \\ = \frac{1}{(1+ e^{-z^{[2]}})} * (1-\frac{1}{(1+ e^{-z^{[2]}})}) \\\] \[\boxed{ \begin{equation*} \frac{\partial A^{[2]}}{\partial Z^{[2]}} = A^{[2]}*(1-A^{[2]}) \end{equation*} }\] \[\frac{\partial L}{\partial Z^{[2]}} = \frac{\partial L}{\partial A^{[2]}} \frac{\partial A^{[2]}}{\partial Z^{[2]}} \\ = \frac{A^{[2]} - Y}{A^{[2]}(1-A^{[2]})} * A^{[2]}*(1-A^{[2]})\] \[\boxed{ \begin{equation*} \frac{\partial L}{\partial Z^{[2]}} = A^{[2]} - Y \end{equation*} }\] \[\frac{\partial Z^{[2]}}{\partial W^{[2]}} = \frac{\partial }{\partial W^{[2]}}(W^{[2]}A^{[1]} + b^{[2]}) = A^{[1]}\] \[\boxed{ \begin{equation*} \frac{\partial L}{\partial W^{[2]}} = \frac{\partial L}{\partial Z^{[2]}} (\frac{\partial Z^{[2]}}{\partial W^{[2]}}) = \frac{\partial L}{\partial Z^{[2]}}A^{[1]} \end{equation*} }\] \[\boxed{ \begin{equation*} \frac{\partial L}{\partial b^{[2]}} = \frac{\partial L}{\partial Z^{[2]}} (\frac{\partial Z^{[2]}}{\partial b^{[2]}}) = \frac{\partial L}{\partial Z^{[2]}} \end{equation*} }\] \[\frac{\partial Z^{[2]}}{\partial A^{[1]}} = \frac{\partial }{\partial A^{[1]}}(W^{[2]}A^{[1]} + b^{[2]}) = W^{[2]} \\ \frac{\partial A^{[1]}}{\partial Z^{[1]}} = \frac{\partial }{\partial Z^{[1]}} (\sigma(Z^{[1]})) = A^{[1]}*(1-A^{[1]}) \\ \frac{\partial L}{\partial Z^{[1]}} = \frac{\partial L}{\partial Z^{[2]}} \frac{\partial Z^{[2]}}{\partial A^{[1]}} (\frac{\partial A^{[1]}}{\partial Z^{[1]}}) = \frac{\partial L}{\partial A^{[1]}}(\frac{\partial A^{[1]}}{\partial Z^{[1]}}) \\\] \[\boxed{ \begin{equation*} \frac{\partial L}{\partial Z^{[1]}} = \frac{\partial L}{\partial A^{[1]}}*g'(Z^{[1]}) \end{equation*} }\]where
\[\frac{\partial L}{\partial A^{[1]}} = \frac{\partial L}{\partial Z^{[2]}}W^{[2]}\] \[g'(Z^{[1]}) = A^{[1]}*(1-A^{[1]})\] \[\frac{\partial L}{\partial W^{[1]}} = \frac{\partial L}{\partial Z^{[1]}} (\frac{\partial Z^{[1]}}{\partial W^{[1]}})\] \[\boxed{ \begin{equation*} \frac{\partial L}{\partial W^{[1]}} = \frac{\partial L}{\partial Z^{[1]}} A^{[0]} \end{equation*} }\] \[\boxed{ \begin{equation*} \frac{\partial L}{\partial b^{[1]}} = \frac{\partial L}{\partial Z^{[1]}} \end{equation*} }\]To summarize all the equation,
\[\begin{equation} W^{[2]} = W^{[2]} - \alpha \frac{\partial L}{\partial W^{[2]}} \end{equation}\] \[\begin{equation} b^{[2]} = b^{[2]} - \alpha \frac{\partial L}{\partial b^{[2]}} \end{equation}\] \[\begin{equation} W^{[1]} = W^{[1]} - \alpha \frac{\partial L}{\partial W^{[1]}} \end{equation}\] \[\begin{equation} b^{[1]} = b^{[1]} - \alpha \frac{\partial L}{\partial b^{[1]}} \end{equation}\]where
\[\begin{equation} \frac{\partial L}{\partial Z^{[2]}} = A^{[2]} - Y \end{equation}\] \[\begin{equation} \frac{\partial L}{\partial W^{[2]}} = \frac{\partial L}{\partial Z^{[2]}}A^{[1]} \end{equation}\] \[\begin{equation} \frac{\partial L}{\partial b^{[2]}} = \frac{\partial L}{\partial Z^{[2]}} \end{equation}\] \[\begin{equation} \frac{\partial L}{\partial Z^{[1]}} = \frac{\partial L}{\partial A^{[1]}}*g'(Z^{[1]}) \end{equation}\] \[\begin{equation} \frac{\partial L}{\partial A^{[1]}} = \frac{\partial L}{\partial Z^{[2]}}W^{[2]} \end{equation}\] \[\begin{equation} \frac{\partial L}{\partial W^{[1]}} = \frac{\partial L}{\partial Z^{[1]}} A^{[0]} \end{equation}\] \[\begin{equation} \frac{\partial L}{\partial b^{[1]}} = \frac{\partial L}{\partial Z^{[1]}} \end{equation}\]Generalized Form
To generalize, for an n layer nerual network,
\[\boxed{ Z^{[l]}=W^{[l]}*A^{[l-1]}+b^{[l]} }\] \[\boxed{ A^{[l]}=g^{[l]}(Z^{[l]}) }\] \[\boxed{ dZ^{[l]}=dA^{[l]}*g'^{[l]}(Z^{[l]}) }\] \[\boxed{ dW^{[l]}=dZ^{[l]}*A^{[l-1]} }\] \[\boxed{ db^{[l]}=dZ^{[l]} }\] \[\boxed{ dA^{[l-1]}=W^{[l]}*dZ^{[l]} }\]